二元变量论证
- 变量之间是可以组合的,组合产生无穷的变化,这是文献复杂的根源
- 两个变量同时代入五恒量,形成5+2结构
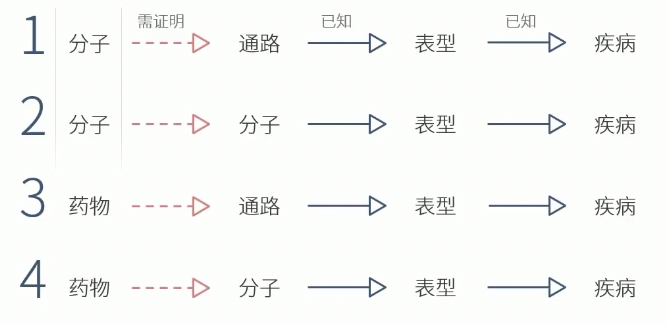
- 常见的二元变量组合套路
- 分子+通路
- 分子+分子
- 药物+通路
- 药物+分子
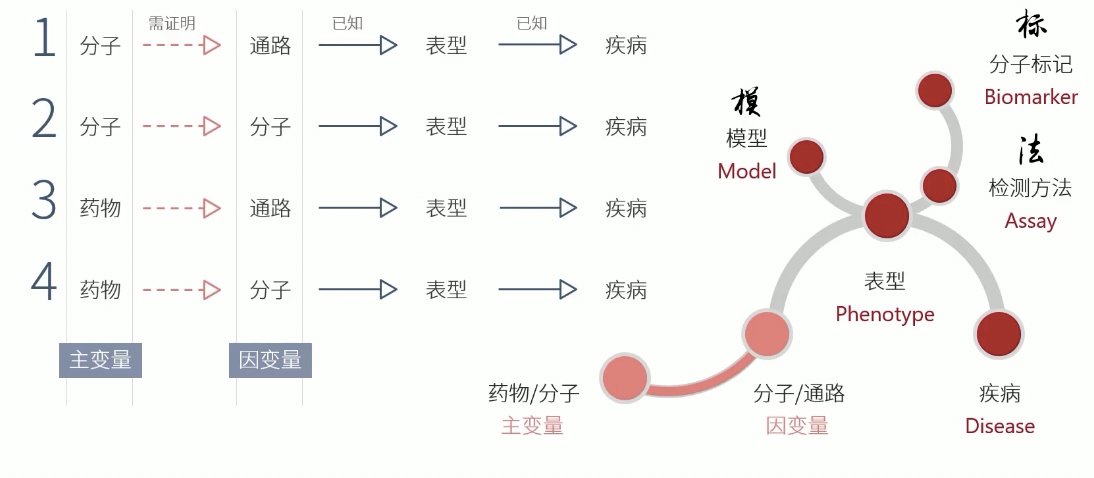
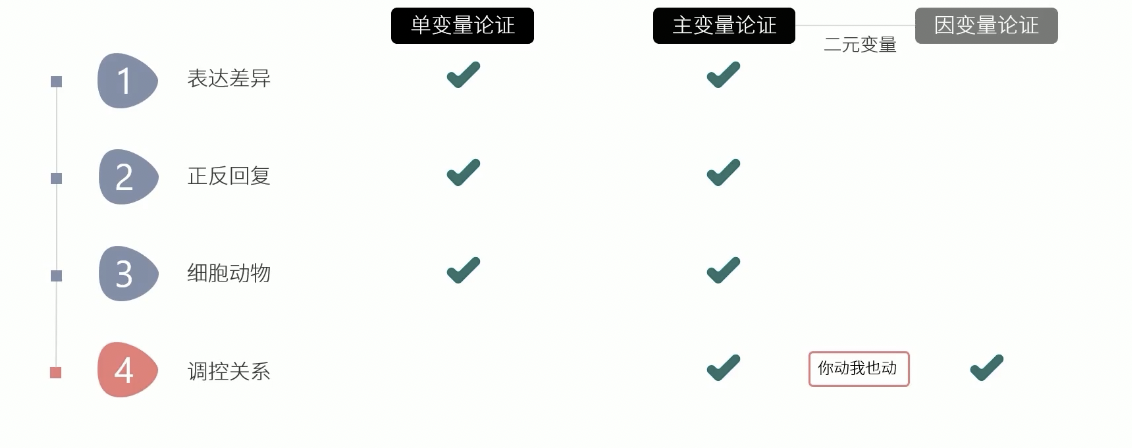
- 谁是主变量,谁是因变量很重
- 主变量承担文章的创新使命,和单变量的表达差异,正反回复,细胞动物套路是一样的
- 因变量是用来解释机制的,大部份情况下因变量和表型之间的关系是已知的,有文献报道
- 通路打死不做主角
- 药物打死不做配角
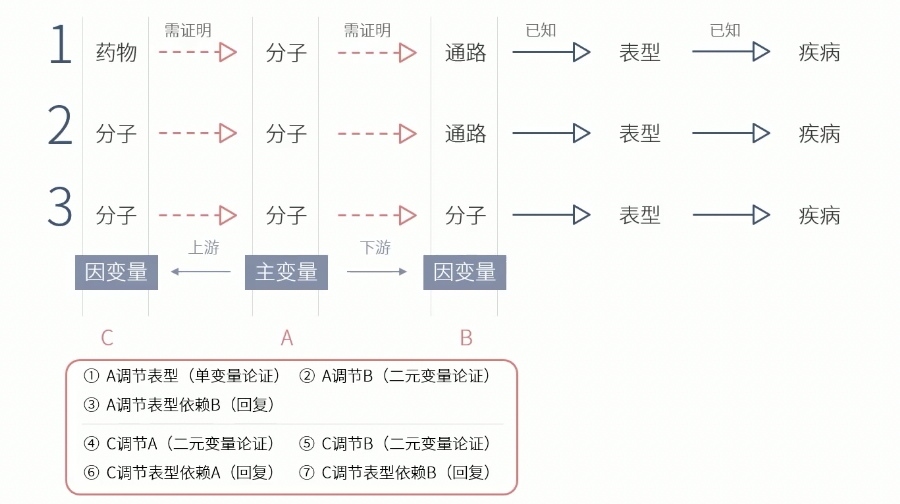
- 完整的二元论证需要4条证据
- 主变量A调节表型(充分性证明)
- 主变量A调节因变量B(二元变量论证,充分性证明)
- 因变量B调节表型(已知或单变量,充分性证明)
- 主变量A调节表型依赖B,没B不行(回复,必要性证明)
逻辑论证主次
主次和上下游没有必然联系
回复验证可以加分(我不动,你动也白动),操作上有的同时,把下游的变化阻断掉,看上游的变化会不会因此改变表型
回复实验策略
- 人为改变两个变量的水平,而改变的趋势和他们原来的调控关系相反
- Step 1:
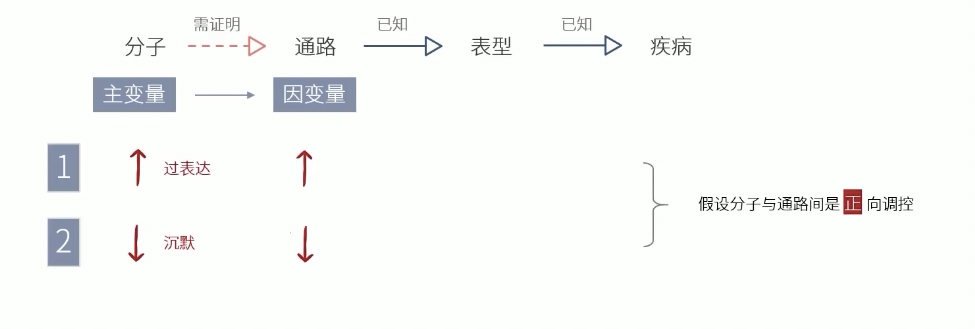
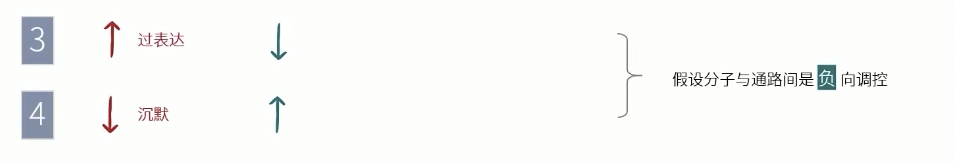
- Step 2:
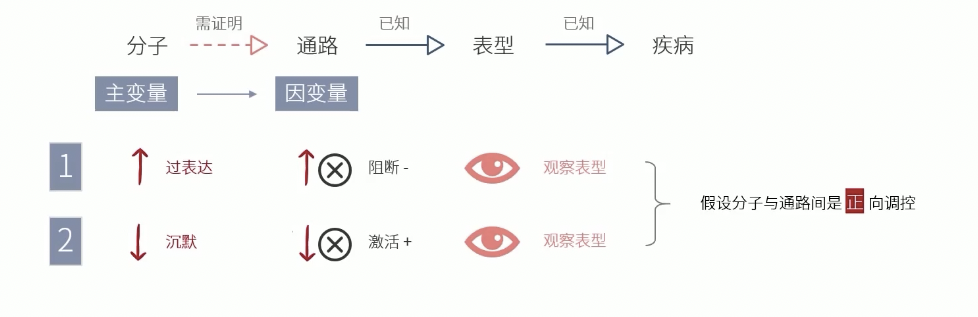

- 正正反,正反正;反正正,反反反
- 第一个正反:上下游分子之间的调控关系
- 第二个正反:对上游分子的调控策略
- 第三个正反:对下游分子的调控策略
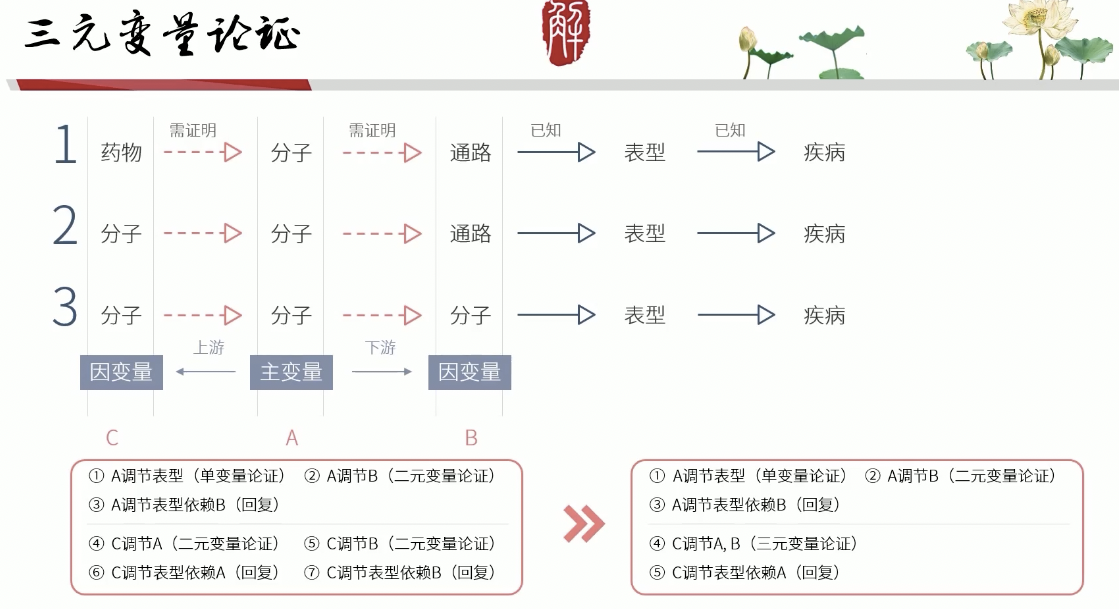
三元变量论证
- 对文章的提升效果其实很有限,因为加上去的因变量别人报道过,没有太大的创新
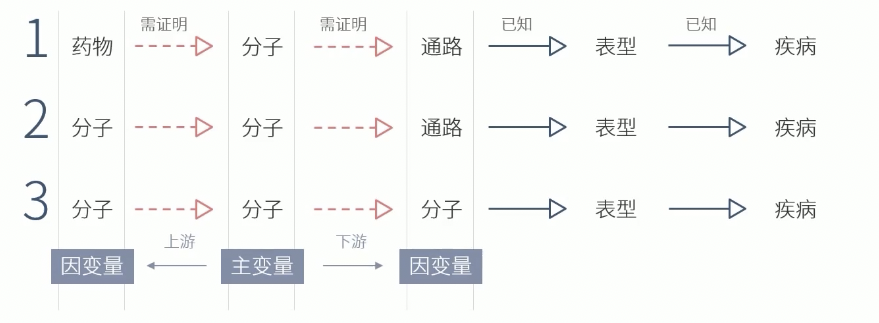
- 围绕主变量的上下游设计因变量的三元变量结构,这才是最完美的课题设计
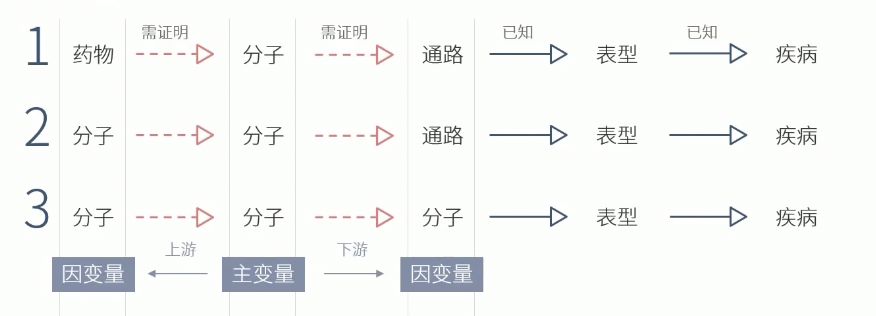
* 一方面回答了下游效应的环节
* 另一方面解答了上游的驱动因素
* 有头有尾,很完整
* 发到TOP CNS也有帮助了
* 二元论证是三元论证的基础